The first condition of equilibrium is that the up forces must equal the down forces and the forces to the right must equal the forces to the left. This is the condition for both static and dynamic equilibrium.
The second condition of equilibrium is rotational equilibrium and exists when a system that could be rotating is either not rotating or rotating at a constant rate. You might think of this as static and dynamic rotational equilibrium.
A point or axis can be chosen as a stationary position that everything rotates around. The force needed to cause rotation depends on the distance from the rotation axis. The distance from the rotation axis to the point where the force is applied is called the lever arm, l. The torque, τ, is a measure of the ability of a force to cause rotation and depends on the perpendicular force, Fn, and the lever arm, l. The torque is equal to the perpendicular force times the lever arm.
τ = Fnl
The direction of the torque is obtained by the right-hand rule, which states that if the fingers ofthe right hand are bent to point along the direction that rotation will occur, the thumb will point in the direction of the torque. Notice that the torque is always perpendicular to the plane of rotation. There are only two possible directions and they would be opposite each other: in and out. In order to be in equilibrium the torque "in" must equal the torque "out", where in would be into the plane of rotation and out would be out of the plane of rotation.
In previous chapters, many objects were considered massless, while others were treated as if they had no shape and were concentrated at a single point, i.e. the point of interest in force diagrams. The single point is called the center of gravity. For symmetrical objects the center of gravity is the geometrical center. For other objects it is the point where the effect of gravity is the same, independent of how the object is rotated. This concept allows the weight of an object to be treated as a force applied at the center of gravity.
A massless meterstick has two boxes hanging from it. One box is 0.2 kg and is placed at the 0.1 m mark, while the other box has an unknown mass and is placed at the 0.6 m mark. A fulcrum, f, is placed at the 0.4 m mark. (a) What upward force does the fulcrum exert? (b) What is the mass of the unknown box?
In torque problems the first thing to decide is where to put l = 0. The decision is made by considering what you know and what you want to determine. If there is an unknown force that we aren't interested in, then it would be a good choice to put l = 0 at the point of that force. That would make the torque equal to zero at that point and we wouldn't have to worry about the unknown force. Sometimes it is easier to put it at the end or middle of a meterstick. It can be any place, but some choices make the math easier than others.
After deciding where l = 0 we apply the two conditions of equilibrium: balanced forces and balanced torques.
The first condition of equilibrium says that the up forces must equal the down forces and the right forces must equal the left forces. In this problem there are only up and down forces, so the force of the fulcrum going up, call that Ff must equal the force due to gravity on the 0.2 kg box, call that F1, plus the force due to gravity on the unknown box, call that F2. We don't know the force at the fulcrum or the force of the unknown mass, so we will come back to this after considering the torques.
The second condition of equilibrium says that the torques in must equal the torques out. If we place the l = 0 at the fulcrum it will eliminate the unknown fulcrum force from the torque equation and leave us with only one unknown, the force due to the unknown mass.
τin = τout
To use the right-hand rule, place your hand at the point where l = 0, which is at the fulcrum in this case, and bend your fingers in the direction that the force being considered would cause the system to rotate. For F1 that would mean the meterstick would rotate counter-clockwise. Your thumb then points in the direction of the torque. For F1 it would be out of the paper. For F2 the rotation would be clockwise and the torque would be into the paper. Remembering τ = Fnl gives:
Fn2l2 = Fn1l1
Since F1 and F2 are directly downward and are due to gravity, Fn1 = m1g and Fn2 = m2g which gives:
m2gl2 = m1gl1
The acceleration due to gravity, g, cancels out, m1 = 0.2 kg, l1 = 0.4 m - 0.1 m = 0.3 m, and l2 = 0.6 m - 0.4 m = 0.2 m. This results in:
m2(0.2 m) = (0.2 kg)(0.3 m)
m2 = (0.2 kg)(0.3 m)/(0.2 m) = 0.3 kg
Now that we know the second mass, we can use the first condition of equilibrium to find the force applied at the fulcrum.
Ff = F1 + F2 = (0.2 kg)(9.8 m/sec²) + (0.3 kg)(9.8 m/sec²) = 4.9 N
A 30 N uniform board is leaned against a smooth vertical wall, creating a 60° angle between the wall and the board. A 20 N mass is placed one-forth of the way up the board from the floor. (a) What force, Fw does the wall exert on the board? (b) What force, Ff must friction at the bottom of the board exert in order to keep the board from slipping?
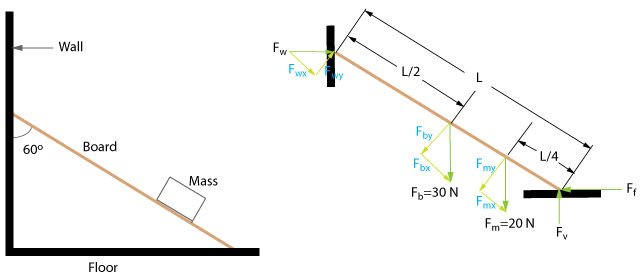
As in the last example, this problem will be solved in two parts. The first part will apply rotational equilibrium (balanced torques) and the second part will apply translational equilibrium (balanced forces).
Assume the point of rotation (the point where l = 0) is at the intersection of the floor and the board. This will eliminate two forces, the vertical force, Fv, and the frictional force, Ff. The torques along the board will be considered. Remember that only the force components that are perpendicular to the board is used when calculating torques along the board (only those labeled as y-components in the diagram). The equation for rotational equilibrium is:
τin = τout
(Fwy)(L) = (Fmy)(L/4) + (Fby)(L/2)
(Fwsin30)(L) = (Fmsin60)(L/4) + (Fbsin60)(L/2)
The length of the board, L, cancels out and Fw is found to be:
Fw = 34.64 N
Using translational equilibrium the following relationships are found:
Forces up = Forces down: Fv = Fb + Fm
Forces left = Forces right: Ff = Fw
The second relationship provides the solution to our problem: Ff = 34.64 N
Model Problem #39Problem: a movie stunt woman of weight 700 N walks out to the end of a uniform horizontal plank that projects perpendicularly over the edge of a roof. The plank is 6 m long and weighs 500 N. How far from the roof can the plank overhang?
Let x be the length of the overhang, from the side of the building to the end of the plank.
ΣF = 0 ⇒ F = 500 N + 700 N = 1200 N (The upward force at the edge of the building.)
Στ = 0 when l = 0 at the person
⇒ (1200 N)(x) = (500 N)(3 m) ⇒ x = 1.25 m
Στ = 0 when l = 0 at the edge of the building
⇒ (700 N)(x) = (500 N)(3 m - x) ⇒ x = (1500 N-m)/(700 N + 500 N) = 1.25 m
Στ = 0 when l = 0 at the center of the plank.
⇒ (700 N)(3 m) = (1200 N)(3 m - x) ⇒ x = (3600 N-m - 2100 N-m)/(1200 N) = 1.25 m
Στ = 0 when l = 0 at the end of the plank over the building.
⇒ (500 N)(3 m) + (700 N)(6 m) = (1200 N)(6 m - x) ⇒ x = 1.25 m